Search for a command to run...
I am currently working as SDE2 at Microsoft & have 3+ years of industry experience.
Have exposure to delivering products both in Open source culture and in a mature corporate setup.
I enjoy weight lifting and reading in my free time.
No comments yet. Be the first to comment.
Code Stories: An Introduction Making Computer Science simple bit by bit If you can’t explain it simply, you don’t understand it well. Computer Science is often seen as an esoteric discipline. Most of the learners approach it in a convoluted fashi...
A few weeks ago, I stumbled upon an interesting problem.In Linux, if you check the file permissions you will notice the name of the file owner along with the group which owns the file. Note that, It is not necessary for the owner to be a part of the ...
The web is an interesting place, it humbles you down and shows how little you actually know. While hitchhiking through the hyperlinks, I had one such realization recently.
What if I ask you to calculate the square root of a number? Depending upon your background you are likely to come up with a variety of solutions. Let me talk about that specific fraction of you who will be interested in churning out code for doing so. [No, sqrt()]
Binary Search seems to be a valid and intuitive approach, after all, we can easily discard half of the search space in each iteration. But I want you to hold that thought and glance over this small snippet below.
double sq(double num)
{
double xn = num/2;
while(abs((xn*xn)-num)>eps) //eps is precision
{
xn = (xn + num/xn)/2;
}
return xn;
}
Magical isn't it? When I first looked at this, I was really startled by the elegance of this solution. So what is it and why does it work?
You just witnessed the glamour of Newton Raphson method.
In simple terms, it is a way to quickly find a good approximation for the roots of a real-valued function f(x) = 0.
This is our cue, square root for a number can be minimally represented by solving for the roots of f(x) = x^2- N, where N is the number we have to find the root of.
That is all cool! But how does it actually work? Let's look at the simple math behind this:-
Consider a general function: y = f(x)
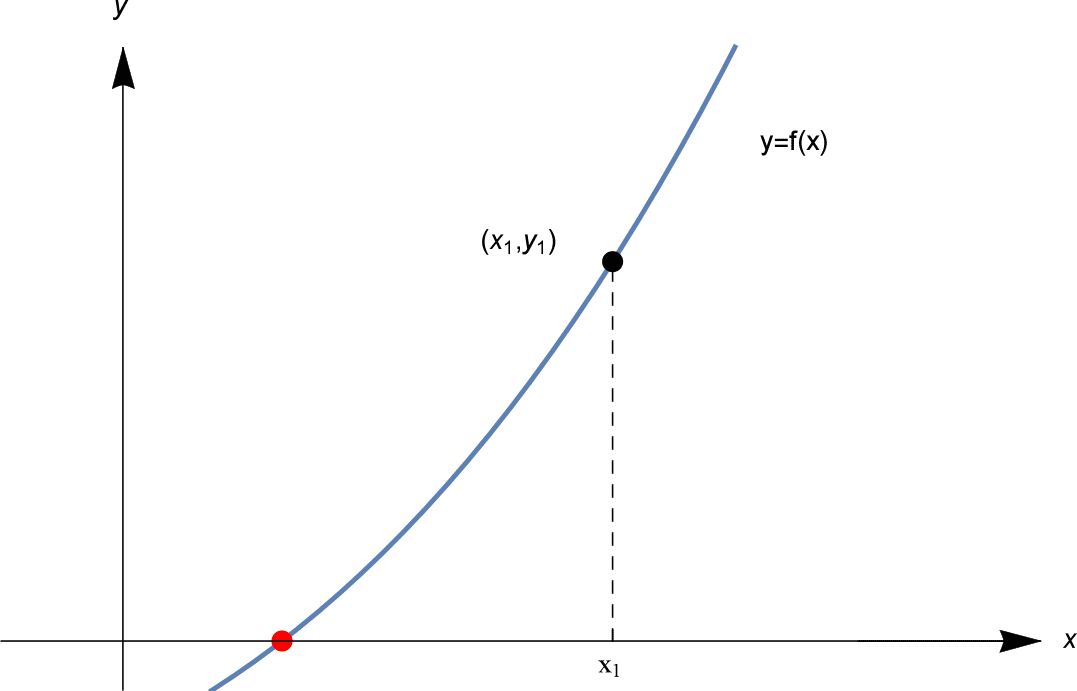We start by choosing an arbitrary value x1 as our starting point[1]. For our specific case, we can choose N/2 as our starting point and can safely discard values greater than that from the candidature of √N.
Now let's draw a tangent (Differential) to the curve at that point and mark its intersection with the x-axis. Let's call this x2.
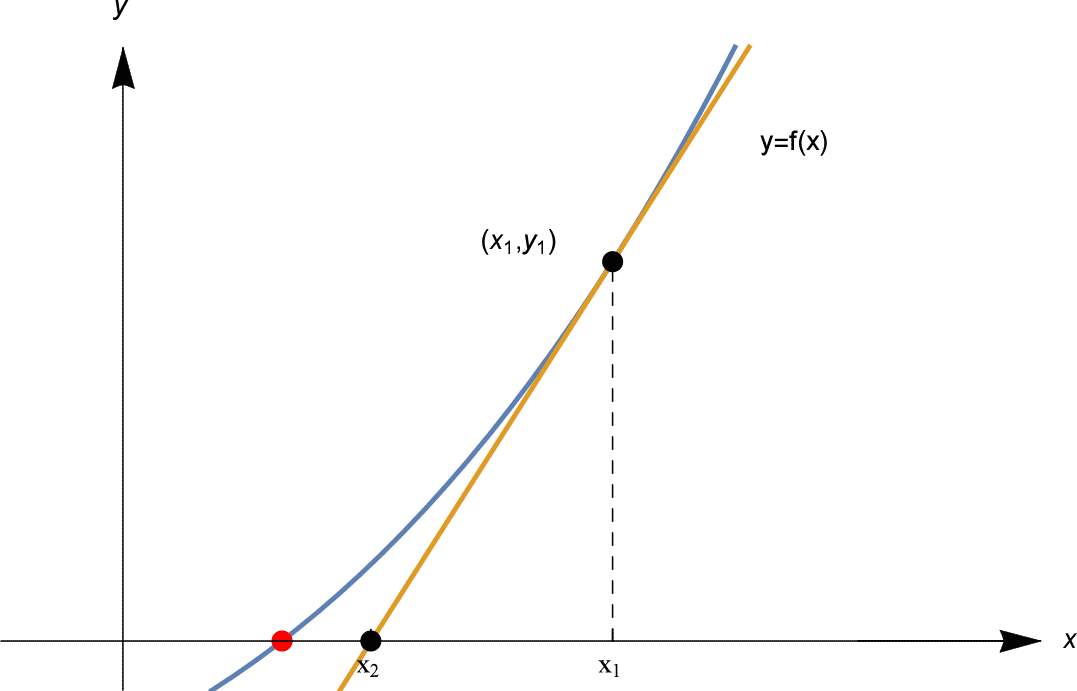
Repeat step 2 for point x2 to obtain x3. You must have noticed that with each iteration we are nearing the roots of the quadratic equation. Slow and steady!
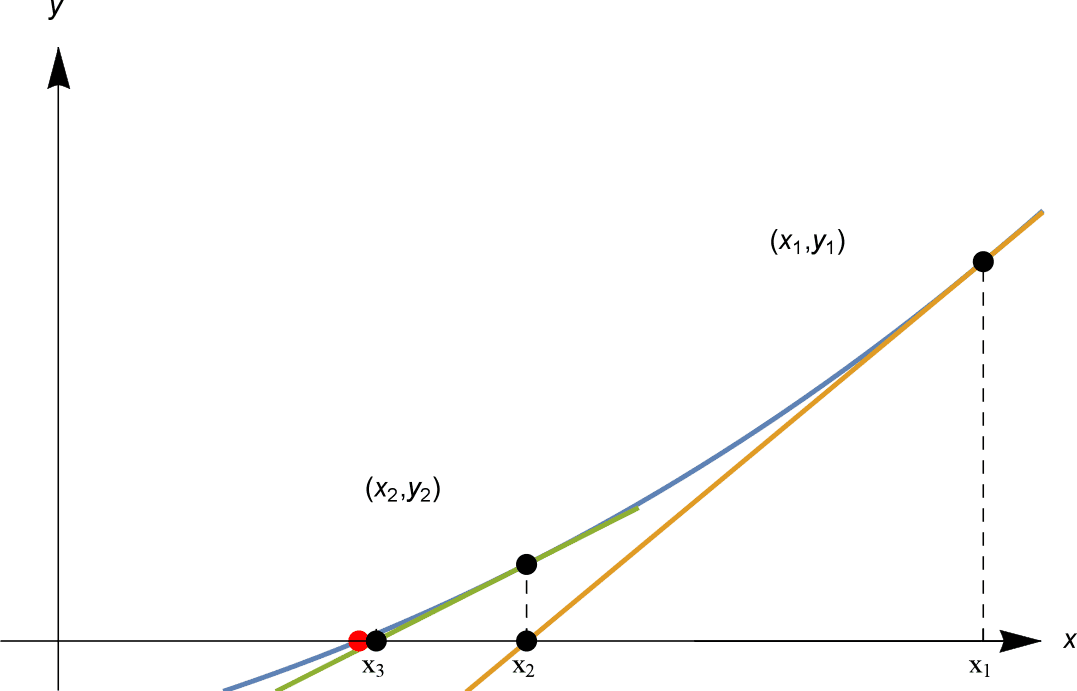Depending upon the precision, you can decide upon the number of iterations required.
Let's try to workout an elegant formula for f(x) = x^2 - N which will get us the compact code we saw in the beginning. Please note that we are aiming to get a relation between N and (N+1) iteration.
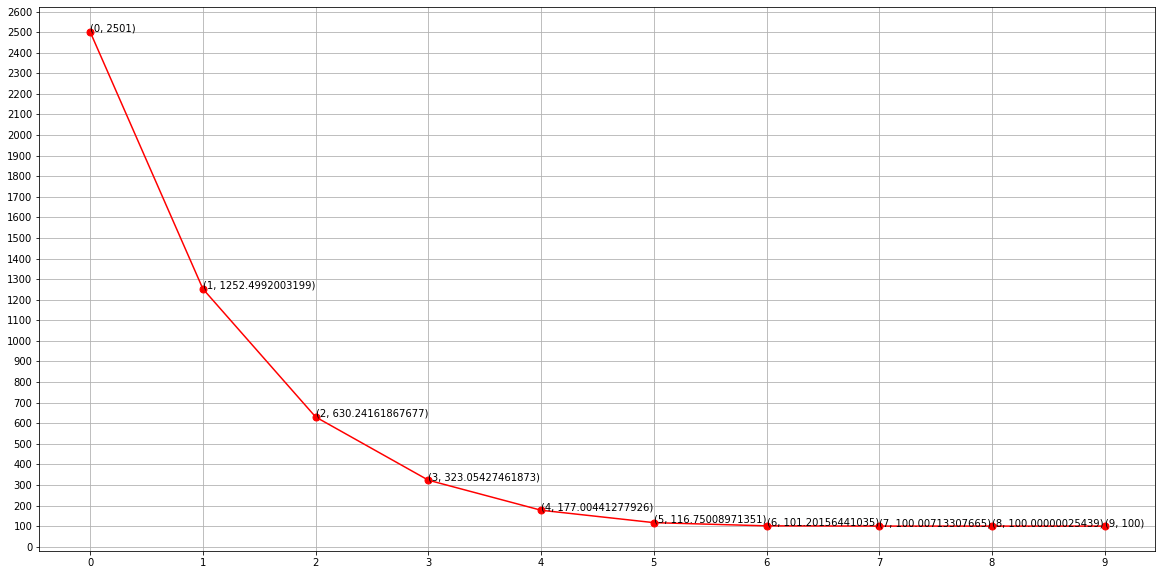
Visualising Newton Raphson method for N = 10000
[1] For the sake of simplicity, I have omitted the details about choosing the initial value which plays a crucial role in more complex functions.
Special thanks to AMSI for facilitating illustrations
If you liked this post, you can find more by:
Following me on Twitter: @abshekha
Connecting on LinkedIn: abhimanyubitsgoa
Visiting my website: https://abhimanyutimes.com
Thanks for reading!